Significance Levels for Multiple Tests
by
Sergiu Hart and Benjamin Weiss
Abstract
Let
X1, ..., Xn
be n random variables, with
cumulative distribution functions
F1, ..., Fn.
Define 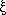 i :=
Fi(Xi) for all i, and let
i :=
Fi(Xi) for all i, and let
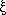 (1)
(1)
 ...
...

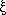 (n)
be the order statistics of the
(
(n)
be the order statistics of the
(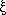 i)i.
Let
i)i.
Let
 1
1
 ...
...

 n
be n numbers in the interval [0,1]. We show that the probability
of the event R :=
{
n
be n numbers in the interval [0,1]. We show that the probability
of the event R :=
{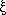 (i)
(i)

 i
for all
1
i
for all
1  i
i  n} is at most
mini{n
n} is at most
mini{n i/i}.
Moreover, this bound is exact: for any given n marginal
distributions
(Fi)i, there exists a joint
distribution with
these marginals such that the probability of R is exactly
mini{n
i/i}.
Moreover, this bound is exact: for any given n marginal
distributions
(Fi)i, there exists a joint
distribution with
these marginals such that the probability of R is exactly
mini{n i/i}.
This result is used in analyzing the significance level of multiple
hypotheses testing. In particular, it implies that the Rüger tests
dominate all tests with rejection regions of type R as above.
i/i}.
This result is used in analyzing the significance level of multiple
hypotheses testing. In particular, it implies that the Rüger tests
dominate all tests with rejection regions of type R as above.
(Check
"Notes on using HTML to present math" by
Martin J. Osborne, to
see how this abstract was produced; thanx, Martin!).
Statistics and Probability Letters
35 (1997), 43-48.
The paper is available for downloading:
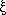 i :=
Fi(Xi) for all i, and let
i :=
Fi(Xi) for all i, and let
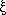 (1)
(1)
 ...
...

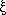 (n)
be the order statistics of the
(
(n)
be the order statistics of the
(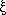 i)i.
Let
i)i.
Let
 1
1
 ...
...

 n
be n numbers in the interval [0,1]. We show that the probability
of the event R :=
{
n
be n numbers in the interval [0,1]. We show that the probability
of the event R :=
{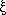 (i)
(i)

 i
for all
1
i
for all
1  i
i  n} is at most
mini{n
n} is at most
mini{n i/i}.
Moreover, this bound is exact: for any given n marginal
distributions
(Fi)i, there exists a joint
distribution with
these marginals such that the probability of R is exactly
mini{n
i/i}.
Moreover, this bound is exact: for any given n marginal
distributions
(Fi)i, there exists a joint
distribution with
these marginals such that the probability of R is exactly
mini{n i/i}.
This result is used in analyzing the significance level of multiple
hypotheses testing. In particular, it implies that the Rüger tests
dominate all tests with rejection regions of type R as above.
i/i}.
This result is used in analyzing the significance level of multiple
hypotheses testing. In particular, it implies that the Rüger tests
dominate all tests with rejection regions of type R as above.