בסעיף
זה נתבונן בפונקציות
![]() שונות,
ונשווה
בין הגרפים שלהן לגרפים של פולינומי
הטיילור שלהן
שונות,
ונשווה
בין הגרפים שלהן לגרפים של פולינומי
הטיילור שלהן
![]() (
(![]() שהוגדר
ב-
6.6).
שהוגדר
ב-
6.6).
פגשנו
כבר בדוגמה זו בסעיף 6.5,
שם
ראינו כי
![]() .
.
על פי ההגדרה בסעיף 6.6:
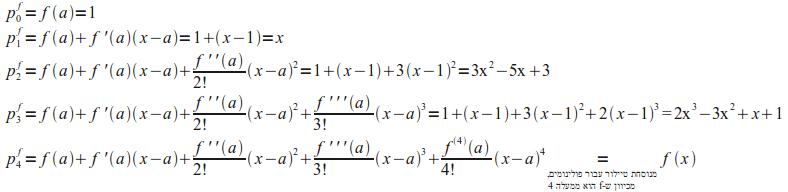
כלומר,
מ-![]() עבור
עבור![]() מתקבלת
סדרת פולינומים ממעלה עולה,
המסתיימת
ב-
מתקבלת
סדרת פולינומים ממעלה עולה,
המסתיימת
ב-
![]() עצמה,
וכך
סדרה זו נותנת הערכות טובות יותר ויותר
ל-
עצמה,
וכך
סדרה זו נותנת הערכות טובות יותר ויותר
ל-
![]() בקרבת
הנקודה
בקרבת
הנקודה
![]() .
.
להלן
מובאים גרפים של 6
הפונקציות:
![]() .
בחן
אותם וראה כי אכן
.
בחן
אותם וראה כי אכן
![]() הינו קירוב טוב יותר ככל ש-
הינו קירוב טוב יותר ככל ש-![]() עולה,
עד
עולה,
עד
![]() .
.
שים
לב כי אם נביט ב-![]() (
(![]() ),
גם
הוא יהיה
),
גם
הוא יהיה
![]() ,
מאחר
ועבור פולינום,
,
מאחר
ועבור פולינום,
![]() ,
כלומר
,
כלומר
![]() .
.
|
|
|
על
מנת למצוא את פולינומי טיילור אנו זקוקים
לערכים של
![]() .
.
מאחר
ש-![]() ,
נקבל
כי
,
נקבל
כי
![]() לכל
לכל
![]() זוגי,
בעוד
עבור כל
זוגי,
בעוד
עבור כל
![]() אי זוגי נקבל לסירוגין
אי זוגי נקבל לסירוגין
![]() ו-
ו-![]() :
:
|
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
0 |
-1 |
0 |
1 |
0 |
-1 |
0 |
1 |
0 |
|
כך
פולינומי טיילור
![]() יהיו:
יהיו:
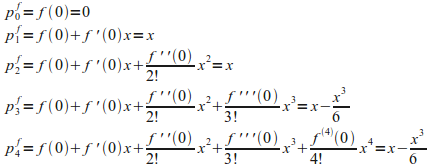
|
אם
נביט בגרפים נראה כי ה"מגע"
בין
הגרף של
|
|
כל
הנגזרות של
![]() הן היא עצמה.
לכן,
הן היא עצמה.
לכן,
![]() ו-
ו-![]() ,
ולכן:
,
ולכן:
|
|
|
הגרפים
של
![]()
![]() מובאים מתחת,
ושוב
ניתן לראות כי הגרפים בין הפונקציה המקורית
לפולינום המקרב הולכים ומתקרבים זה לזה,
על
פני סביבה גדלה והולכת של x-ים
סביב
מובאים מתחת,
ושוב
ניתן לראות כי הגרפים בין הפונקציה המקורית
לפולינום המקרב הולכים ומתקרבים זה לזה,
על
פני סביבה גדלה והולכת של x-ים
סביב
![]() .
.
|
|
|
במקרה
הזה אנחנו צריכים לעבוד קצת יותר קשה על
מנת למצוא נוסחה לנגזרת ה-![]() -ית.
תחילה:
-ית.
תחילה:
|
|
|
נכתוב
זאת כחזקה:
![]() ,
וכעת
יקל עלינו לגזור ביטוי זה שוב ושוב:
,
וכעת
יקל עלינו לגזור ביטוי זה שוב ושוב:
|
|
|
ובאופן
כללי
![]() כך ש-
כך ש-![]() (עבור
(עבור
![]() ).
על
כן:
).
על
כן:
|
|
|
|
|
|
שים
לב כי הפעם,
למרות
שהקירוב של
![]() ל-
ל-![]() משתפר
ככל ש-
משתפר
ככל ש-
![]() גדל
בקרבת
גדל
בקרבת
![]() ,
לא
נראה כי הסביבה [ב-x]
בה
הקירוב מתקרב ל-f
הולכת
וגדלה.
בפרט,
עבור
,
לא
נראה כי הסביבה [ב-x]
בה
הקירוב מתקרב ל-f
הולכת
וגדלה.
בפרט,
עבור
![]() הקירוב אינו טוב בכלל!
מאחר
ו-
הקירוב אינו טוב בכלל!
מאחר
ו-![]() מוגדר
רק עבור
מוגדר
רק עבור
![]() והוא גדול ושלילי ככל ש-
והוא גדול ושלילי ככל ש-
![]() ,
איננו
יכולים לצפות כי הפולינומים
,
איננו
יכולים לצפות כי הפולינומים
![]() יספקו קירוב טוב בסביבת
יספקו קירוב טוב בסביבת
![]() ,
אבל
לכתחילה,
סביב
,
אבל
לכתחילה,
סביב
![]() שום
דבר משונה לא קורה לפונקציה!
(ולכן
לא ברור מדוע הקירוב אינו טוב החל מנקודה
זו)
שום
דבר משונה לא קורה לפונקציה!
(ולכן
לא ברור מדוע הקירוב אינו טוב החל מנקודה
זו)