חומר עזר 6.6 : פולינום טיילור – הגדרה

אם היא פונקציה גזירה פעמים בנקודה , אזי פולינום טיילור של מדרגה (סביב ) הוא הפולינום:

הסימון בו אנו משתמשים עבור פולינום זה הוא כאשר הוא משום האות הראשונה במילה פולינום, היא הפונקציה, ו- מייצג מעלת הפולינום.

הנקודה סביבה אנו מפתחים לא כלולה בסימון זה. לרב נקודה זו קבועה לאורך דיון מסויים.

מוסכמה אם הערך של לא מוזכר, אנו מניחים כי הפיתוח הוא סביב (כלומר אלא אם כן הוגדר אחרת).

הערות

1. כאשר , הוא קבוע – זהו הקירוב הקבוע הטוב ביותר ל- בסביבת .

אם ידוע כי רציפה, אזי אנו יודעים כי ערך הפונקציה ב-x קרוב לערכה ב-a עבור .

2. כאשר , הוא הקירוב הלינארי (הטוב ביותר) ל- בסביבת , כלומר- זו הפונקציה שהגרף שלה הוא הקו המשיק לגרף של בנקודה .

3. באופן כללי, אנו יכולים לגזור את הנוסחה שוב ושוב (כפי שעשינו בפיתוח נוסחת Maclaurin בתת-פרק 6.4).

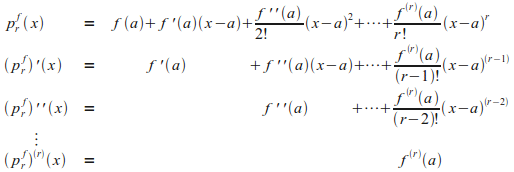
כעת, בהצבת , נוכל לראות כי האיברים היחידים שאינם אפס מגיעים מהאלכסון:

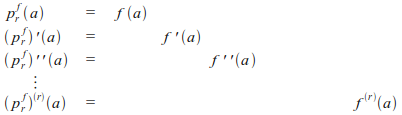
כלומר, הערכים של , וכל הנגזרות שלו עד לנגזרת ה--ית, בנקודה , זהים לאלו של . לכל גזירה נוספת לאחר הגזירה ה--ית, פולינום מדרגה לא יוכל להזדהות עם הערכים הנ"ל (הנגזרות של ), מאחר וכל הנגזרות הגבוהות יותר () של פולינום כזה מתאפסות.

כך הוא הקירוב הפולינומיאלי הטוב ביותר מסדר לפונקציה בסביבת הנקודה , במובן שהערכים שלו ושל כל הנגזרות שלו עד וכולל הנגזרת ה--ית (בנקודה ) זהים לאלו של .

במקרה הספציפי בו היא פולינום ממעלה , לפי נוסחת טיילור

אבל אחרת אנחנו רק יכולים לקוות ל"קירוב טוב".