חומר עזר5.10 : פיתוח נגזרות פשוטות

עתה נשתמש בשלושת החוקים 1,2,3 מ- B5.9 לגזירת סכומים, מכפלות והרכבות, כדי להסיק את הנגזרות של פונקציות אלמנטריות שונות, ממספר תכונות בסיסיות של פונקציות אלה. לגישה מעט יותר ריגורוזית, ראה פרק 5A. מאחר שלא נתנו במסגרת הפרק הנוכחי הגדרות ריגורוזיות לפונקציות sin, cos, ln, exp ברור שבבואנו להוכיח משהו לגבי הנגזרות שלהן נאלץ להגביל עצמנו לשימוש בתכונות העולות מהגדרתן הגיאומטרית \ באינטואיציה.

הפונקציה :

הנגזרת של פונקציית הזהות היא 1, מאחר ש- תמיד, ולכן גם, כלומר.

גיאומטרית, הגרף של הפונקציה x הוא הקו y=x ששיפועו 1, אז זה הערך של הנגזרת (בכל מקום).

כדי לגזור את , נסתכל עליה כמכפלת x-ים

לכן

ואילו

באופן אינדוקטיבי נסיק:

הפונקציה:

כדי למצוא את , נכתוב . אז

נגזור זאת ע"י חוק המכפלה:

כלומר

כלומר לכן

דרך נוספת היא בעזרת עקרונות בסיסיים, כמו שעשינו עבור הפונקציה ב- B5.4. ראה תרגילים.

הפונקציה :

הפונקציה היא הרכבה של f והופכית, אז ניתן להשתמש בכלל השרשרת. נגדיר: :

(או ע"י שימוש ב- “בלוב": )

כלומר

נגזרת של מנה:

נכתוב את המנה כמכפלה . אז:

כלומר

נגזרת של sin:

כאן עלינו לחזור לעקרונות בסיסיים:

כך ש-

אנחנו רוצים להבין מה קורה ל- כש- . מהשורה האחרונה אנו רואים שהתלות של ב- מוגבלת לשני הביטויים:

לכן אנחנו צריכים לדעת מה קורה להם כש- .

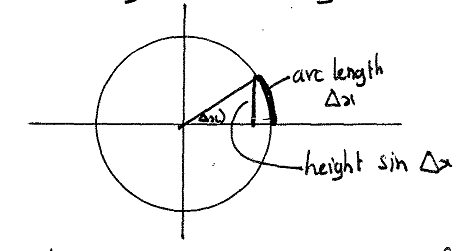
מגיאומטריה אנחנו יודעים ש- לכן . (זה היחס בין הגובה לבין אורך הקשת ).

התוצאה היא ש כאשר ולכן

כלומר

נגזרת של cos:

הטיעון הוא כמעט זהה לטיעון שלעיל לגבי sin. נקבע ואז:

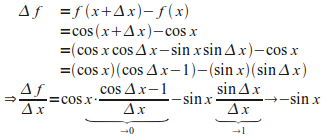
כלומר

נגזרות של פונקציות טריגונומטריות אחרות:

מאחר שכל הפונקציות הטריגונומטריות האחרות (tan,cot,sec,csc) מוגדרות במונחים של sin,cos בעזרת מנות, אפשר לגזור גם אותן עכשיו.

החשובה ביותר מבין אלה היא :

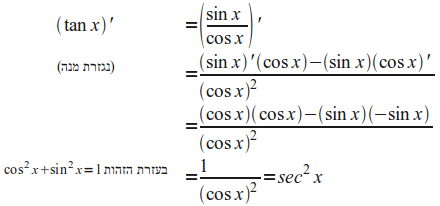
כלומר

הנגזרות האחרות הן:

בגלל ש-

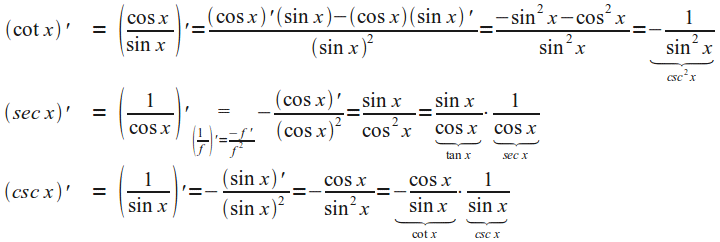
נגזרותיהן של פונקציות מעריכיות:

נתבונן בפונקציה המעריכית כש- a>0 קבוע. מהי צורת הנגזרת? מאחר שלא הגדרנו פונקציות מעריכיות בצורה מאוד ריגורוזית, ובוודאי שלא מהו המספר e, לא נוכל לצפות לקבל נוסחה מלאה לנגזרת של או, אבל ניתן לקבל כמות מפתיעה של מידע (בהנחה שפונקציות אלה גזירות) מתכונותיהן של פונקציות מעריכיות שאנחנו כן מכירים:

אז מה כאן?

התלות ב- מוגבלת כאן לביטוי. כלומר כאשר , ניתן לצפות ש- ישאף לערך כלשהו, נסמנו C, שתלוי ב- a בלבד (רק a מופיע בביטוי – x לא מוזכר). במקרה זה,

כלומר:

הבה נשקול שוב את המשמעות של C ולמה אנו מצפים ש- אכן יתקרב לערך כלשהו כש-.

הביטוי, הוא השיפוע של המיתר שמחבר בין תמונות הנקודות בגרף של f. אז C חייב להיות השיפוע של המשיק ל- ב- x=0. איך הוא תלוי ב- a?

למרות שלא הגדרנו את המספר e, כן הגדרנו

.

זה יתקיים עבור כל בסיס (ובפרט- עבור 2): , כל עוד משתמשים באותו בסיס ללוגריתם (ln או פה) ובאנטי-לוגריתם חזקה (exp או פה). המשמעות של זה היא ש- היא הפונקציה המתקבלת מ- ע"י החלפת x ב-. הגרף של מתקבל אם כן מ- ע"י מתיחה בפקטור שלבכיוון ציר ה- x. כלומר העובדה החשובה היא שכל הגרפים של פונקציות (עבור קבועים a>0) מתקבלים זה מזה ע"י מתיחה בכיוון ציר ה- x (המתיחה עשויה להיות בפקטור שלילי ובמקרה זה הגרף המתקבל לאחר המתיחה בפקטור שלילי יהיה שיקוף ביחס לציר ה- y של הגרף המקורי. זהו המקרה כאשר המעבר הוא בין ערכים של a מהצדדים השונים של 1). יש יוצא דופן אחד: a=1 אבל לכל x, לכן נתעלם ממקרה זה!)

באופן דומה השיפועים של המשיקים ב- x=0 מושפעים ממתיחה זו – מתיחה בפקטור 2 בכיוון ציר ה- x מקטינה שיפוע המשיק פי 2 . התוצאה היא שניתן לצפות לקבל את כל הערכים השונים של C () מערכים שונים של a. דרך אחת להגדיר את e היא לומר שזהו הערך של a עבורו השיפוע של המשיק ל- ב- x=0 הוא 1 (). אז:

מכך אנו יודעים את הערך של C לכל a: הגרף של מתקבל מהגרף של ע"י מתיחה בפקטור בכיוון ציר x, אז השיפוע החדש של המשיק ב- x=0 הוא פעמים השיפוע של exp ב-x=0 (שהוא 1) כלומר ולכן

[סיכום: (החלפת משתנה y ב- למעבר בסיס מ-a ל-b )

החלפת משתנה באה לידי ביטוי במתיחה פי בכיוון ציר ה-x של הגרף המקורי (כפי שנוכחנו בפרק 2)

מתיחה פי של הגרף בכיוון ציר ה-x משנה שיפוע המשיק ב-x=0 באופן הבא: ]

הפונקציה מסומנת גם .

לחילופין ניתן להשתמש בכלל השרשרת ישירות: