חומר עזר 1.11 : מכפלה סקלרית של שני וקטורים, הגדרה

נציג עכשיו פעולה חדשה על וקטורים הקרויה מכפלה סקלרית.

נבדיל בין מכפלה סקלרית (Scalar product) לבין מכפלה של וקטור בסקלר (Scalar multiple):

במקרה הראשון, כפל בסקלר, המונח סקלר מתייחס לכופל, ואילו במקרה של מכפלה סקלרית,

המונח סקלר מתייחס לעובדה שהמכפלה (התוצאה) היא סקלר, בניגוד למכפלה וקטורית (ראה 1.16)

שתוצאתה היא וקטור.

כבעבר, נגדיר את הפעולה בעזרת רכיבי הווקטורים הנכפלים:

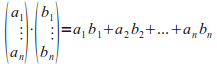
סימון: מכפלה סקלרית נקראת גם מכפלה פנימית (Inner product) או Dot product.

למכפלה זו אופני סימון רבים. נסמן את המכפלה הסקלרית של כך (ומכאן השם- dot product- משום הנקודה).

סימונים נוספים בשימוש נפוץ: .

דוגמאות:

א. בדו-מימד (n=2) נקבל:

ב. בתלת-מימד (n=3) נקבל:

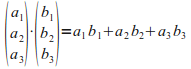
ג.

* נשים לב שהתשובה היא אכן סקלר.

ד.

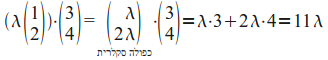
א. תכונות של מכפלה סקלרית:

הערות:

א	אלה נובעות ישירות מהגדרה:
	1.
	2.
	3.
	4.

ב	תכונות 1,2,3 דומות לתכונות המתאימות של כפל של שני מספרים ממשיים:
		1 דומה ל- ab=ba (קומוטטיביות/ חילוף)
		2 דומה ל-(דיסטריבוטיביות/ פילוג)
		3 דומה ל- (אסוציאטיביות/ קיבוץ)
	קיים כמובן הבדל גדול בכך שהתוצאות של המכפלות האחרונות הם תמיד סקלרים בעוד שהם וקטורים והוא סקלר, ולכן אין לכנות תכונה 3 "אסוציאטיביות”. על אף זאת קיום תכונות אלה תומך בכינויסוג של מכפלה.

ג	תכונות 2 ו-3 קובעות כי התלות של ב-היא לינארית. ע"י שימוש בסימטריה (תכונה 1) נוכל לראות שהתלות ב חייבת להיות לינארית גם כן ולכן נוכל לומר שתלוי בובבצורה בי-ליניארית. כלומר, ניתן לפתוח סוגרים באופן הבא: כמו כן נוכל לומר ש-